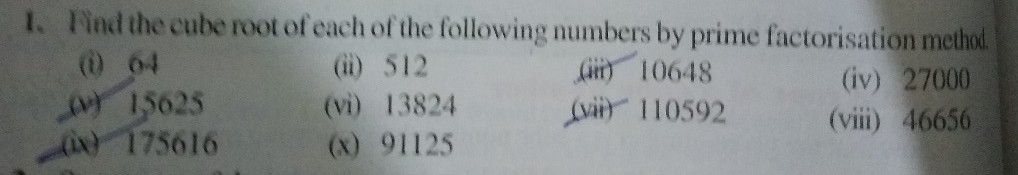Square Root Of 10648

Perfect cube roots table 1 100.

Square root of 10648.

For example 22 is the cube root of 10648 because 22 3 22 22 22 10648 22 is cube root of 10648 because 22 3 22 22 22 10648. Also tells you if the entered number is a perfect square. Square root of 10648. For example 2 is the square root of 4 because 2x2 4.

The nearest previous perfect cube is 9261 and the nearest next perfect cube is 12167. Find the square root or the two roots including the principal root of positive and negative real numbers. For example 22 is the cube root of 10648 because 22 3 22 22 22 10648 22 is cube root of 10648 because 22 3 22 22 22 10648. A cube root of a number a is a number x such that x 3 a in other words a number x whose cube is a.

Since 10648 is a whole number it is a perfect cube. One is positive bigger than zero and the other is negative. Free math problem solver answers your algebra geometry trigonometry calculus and statistics homework questions with step by step explanations just like a math tutor. In other words the square of this number equals ten thousand six hundred and forty eight.

Calculate the positive principal root and negative root of positive real numbers. Definition of cube root. The number 1 is not a prime number but a divider for every natural number. If you have been looking for square root of ten thousand six hundred and forty eight then you are right here too on this page you can also find what the parts of 10648 are called and in addition to the terminology of.

10648 is said to be a perfect cube because 22 x 22 x 22 is equal to 10648. Definition of cube root. Perfect cube roots table 1 100. The square root of 10648 is the number which multiplied by itself is 10648.

What is cube root of 10648. A square root of a number is a number that when it is multiplied by itself squared gives the first number again. See also our cube root table. Only numbers bigger than or equal to zero have real square roots.

Square root calculator and perfect square calculator. See also our cube root table. Your prime factorization is the empty product with 0 factors which is defined as having a value of 1.